傳統方法允許通過簡單支撐梁的均衡模型,基于由一個或兩個軸承支撐的單個軸來估計應用中的軸承載荷,該方法是快速選擇軸承的理想方法,通過對軸幾何結構和操作條件的最少信息,可以評估軸承負載,以適應廣泛的應用。


在上圖所示的示例中,傳統方法可以快速提供每個支架承載的施加載荷(F)的大小,超靜態結構(由兩個以上軸承支撐的軸)不易處理,需要更復雜的模型來評估施加到不同支撐中的力的分布。
在這種方法中,一個主要假設是軸承相對于徑向位移是無限剛性的,并且它們不提供旋轉阻力,由于不需要軸承的內部幾何形狀,因此假設加載的滾動元件覆蓋約180度的載荷區,而無需進一步詳細計算。
傳統方法對軸承剛度(=位移和旋轉阻力)的假設有時候并不精確,并非所有軸承類型都適合大旋轉或大軸向偏移,為了更好地了解軸承的性能,了解其內部幾何結構非常重要。
軸承剛度是軸承箱方法中考慮的基本問題之一,最終平衡取決于幾個組合剛度貢獻,即軸、殼體和軸承,由于每一個千分尺都計數,因此軸承性能的準確評估也取決于實際操作條件,尤其是轉速和溫度,此外,用于將軸承固定在軸上和殼體座內部的配合也是一個極其重要的因素,配合、轉速和溫度從最初的軸承制造間隙嚴重改變為運行間隙(另見間隙減小)。
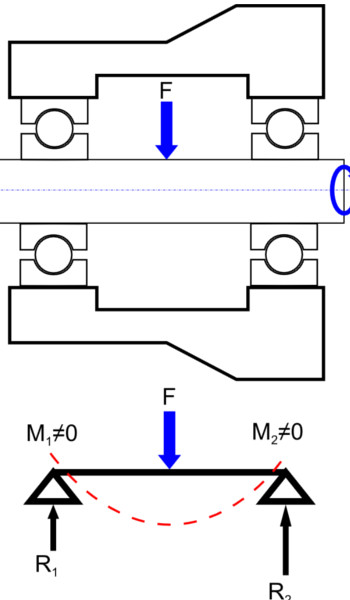

如上圖所示,通過考慮軸承的真實內部幾何形狀以及軸和殼體的幾何形狀和安裝配合,這種系統的解決方案不是傳統方法所建議的,不同的殼體幾何形狀和可能的配合,右軸承可能會填充更大的間隙減小;工作內部間隙不同,左右軸承可能呈現不同的剛度;滾珠軸承提供的有限旋轉剛度,軸承產生彎曲力矩;內部間隙不同,即使負載位于軸的中間,軸承負載條件也可能不同。


